The Socratic Method for Self-Discovery in Large Language Models
| May 5, 2023 | Written by Runzhe Yang and Karthik Narasimhan |
“…Do you see what a captious argument you are introducing — that, forsooth, a man cannot inquire either about what he knows or about whit he does not know? For he cannot inquire about what he knows, because he knows it, and in that case is in no need of inquiry; nor again can lie inquire about what he does not know, since he does not know about what he is to inquire.”
— Plato, Meno (385 BCE)
In this blog post, we explore three key aspects that hold immense potential in unleashing the capabilities of Language Model models (LLMs):
-
Multi-Agent Collaborative Problem Solving (with Human in the Loop)
We delve into the fascinating realm of multi-agent collaborative problem solving, with both LLM-based agents and humans involved in the process. By assigning distinct roles to LLMs, such as ‘analysts’ or ‘proofreaders’, we can effectively leverage their unique strengths and enhance their overall capabilities as a team of agents. -
The Power of the Socratic Method
We examine the Socratic method and its ability to robustly elicit analytical and critical thinking capabilities in LLMs. While approaches like CoT/ReAct have made strides in this area, they often rely on a fixed form of meticulously crafted prompting. We propose alternative strategies fostering free-form inquiry among agents to fully unlock the potential of LLMs. -
Rethinking ‘Prompting’ for Knowledge and Reasoning
We generalize the concept of “prompt engineering” to a more comprehensive approach. Rather than relying on a small number of fixed prompt formats to guide text generation, we advocate for leveraging the inherent reasoning capabilities of LLMs through autonomous, free-form dialogue among the LLMs themselves. Our preliminary exploration demonstrates that LLMs can engage in autonomous dialogue, allowing them to self-discover knowledge and expand their perspectives, leading to a broader spectrum of insights for solving the problem at hand.
Based on these insights, we propose SocraticAI, a new method for facilitating self-discovery and creative problem solving using LLMs.
The SocraticAI framework involves the participation of multiple language model-based agents in a Socratic dialogue aimed at solving a problem proposed by the user. Further details are introduced in the article below.
- Platonic epistemology: all learning is recollection.
- Large Language Models: all you need is prompting.
- Socratic dialogues among LLMs
- Future & Limitations: envisioning a collaborative AI society
Platonic epistemology: all learning is recollection.
Within the hallowed corridors of ancient Athens in 402 BCE, Socrates, the Greek philosopher, and Meno, a wealthy Thessalian leader, engage in a dialogue to explore the genesis of virtue. During their discourse, Socrates unveils a bold assertion, “All learning is recollection.” This provocative proposition, also known as the theory of anamnesis, posits that our souls are imbued with knowledge from past lives and that learning is simply the process of unearthing this dormant wisdom.
Plato later immortalizes their conversation in Meno.
To illustrate the idea of anamnesis, Socrates presents Meno’s servant boy with a geometric problem, asking him to double the area of a 2x2 square (Plato, Meno, 82a-85e). With no prior expertise in math, the boy first suggests doubling the sides of the square, but after a series of simple questions, he realizes that this results in a square four times larger than the original:
Socrates: Now watch his progress in recollecting, by the proper use of memory. Tell me, boy, do you say we get the double space from the double line? The space I speak of is not long one way and short the other, but must be equal each way like this one, while being double its size—eight square feet. Now see if you still think we get this from a double length of line.
Boy: I do.
Socrates: Well, this line is doubled, if we add here another of the same length?
Boy: Certainly.
Socrates: And you say we shall get our eight-foot space from four lines of this length?
Boy: Yes.
Socrates: Then let us describe the square, drawing four equal lines of that length. This will be what you say is the eight-foot figure, will it not?
Boy: Certainly.
Socrates: And here, contained in it, have we not four squares, each of which is equal to this space of four feet?
Boy: Yes.
Socrates: Then how large is the whole? Four times that space, is it not?
Boy: It must be.
Socrates: And is four times equal to double?
Boy: No, to be sure.
Socrates: But how much is it?
Boy: Fourfold.
......
The above dialogue is excerpted from Meno, not generated by LLMs :)
Having grasped the previous insight, the boy then suggests extending the sides by half their length, leading Socrates to ask another series of questions that help the boy recognize that would create a 3x3 square. The boy admits his confusion and inability to proceed. Undeterred, Socrates persistently prompts the boy through a series of simple, step-by-step questions, eventually navigating him to the correct solution: using the diagonal of the original square as the base for the new square.
The crux of this theory: despite the boy’s lack of mathematical expertise, Socrates leads the boy to “recollect” the solution to the problem by asking the right questions. This captivating story not only highlights the potential of the Socratic method but also embodies its notion that learning is a process of self-discovery (or recollection) of innate knowledge.
Large Language Models: all you need is prompting.
Fast forward to the present, where large language models (LLMs) have emerged as the prodigies of artificial intelligence. LLM-based AI systems, such as OpenAI’s ChatGPT, are vaguely reminiscent of Meno’s servant boy, who possesses vast amounts of “innate” knowledge and problem-solving abilities, but only needs the right prompts to reveal them.
These language models are pre-trained on massive datasets, learning to predict the next word in a sequence, and then fine-tuned with few instructions and feedback. As the model size and data set size increase, LLMs obtain many “emergent” abilities (Kaplan et al., 2020; Schaeffer et al., 2023), such as zero-shot or few-shot generalization ability and reasoning. The pre-training process of LLMs is akin to the “past lives” in Socrates’ theory.
In Meno, the boy confidently suggests an incorrect solution at the beginning, but Socrates skillfully guides him with thoughtfully constructed questions. Similarly, LLM-based AI systems may sometimes “hallucinate,” producing seemingly reasonable yet incorrect or nonsensical responses. To fully unlock the potential of LLMs, “prompt engineering” becomes essential. Various techniques, including “Chain of Thought” (CoT) (Huang et al., 2022; Wei et al., 2022), “Describe, Explain, Plan, and Select” (DEPS) (Wang et al., 2023), “Reason+Act” (ReAct) (Yao et al., 2023) and self-reflection (Reflexon) (Shinn et al., 2023) have been developed to augment LLMs’ problem-solving capabilities through multi-step planning and articulated reasoning processes.
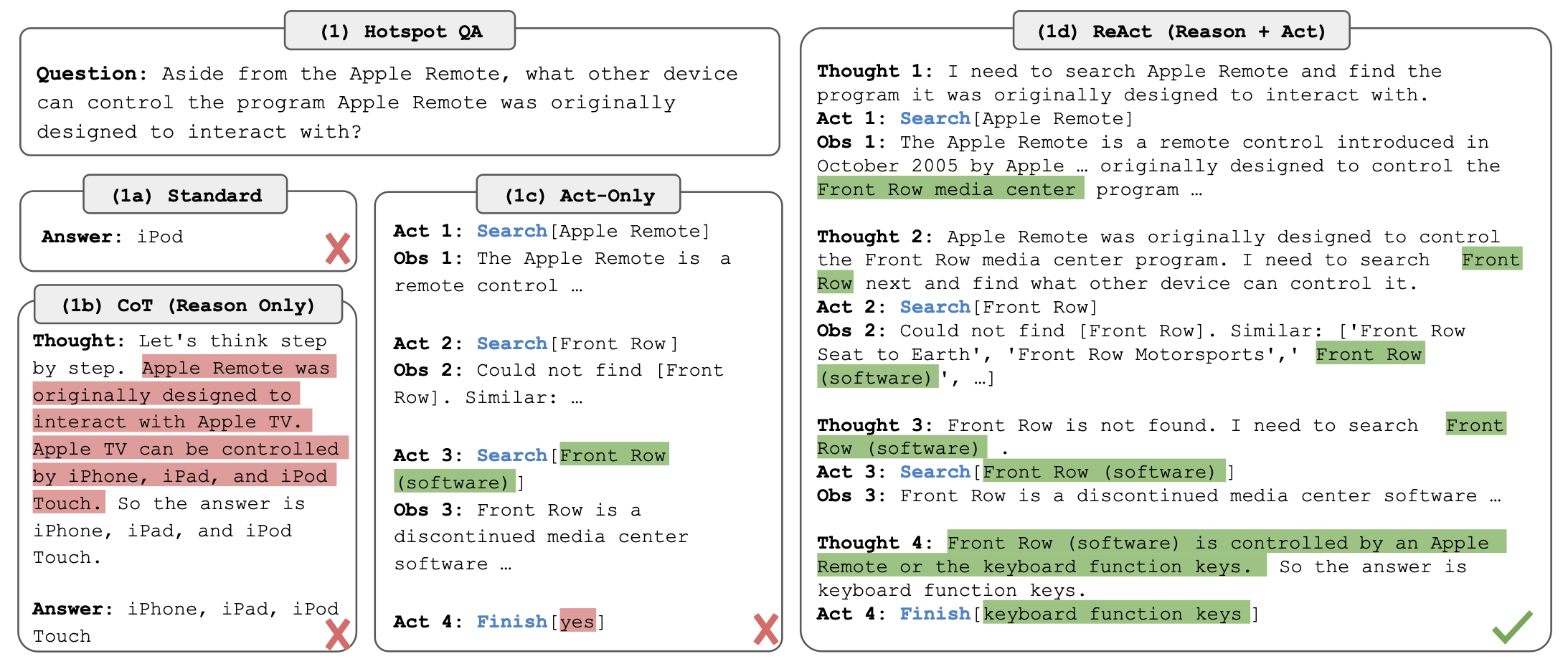The LLM hallucinates with incorrect answers. With appropriate prompting methods such as ReAct, the LLM is able to generate the correct answer. (Figures modified from Yao et al., 2023)
As remarkable as these prompt engineering techniques are, they 1) require the creation of task-specific prompt templates, and 2) are limited to a single train of thought within the LLM which precludes the use of multiple attack angles for creative problem solving (as we demonstrate in examples below). Given the similarities between modern-day LLMs and the boy in Meno, one cannot help but wonder if the Socratic dialogue method could be adapted to involve multiple LLMs in conversation, with the AI system also playing the role of Socrates and guiding the other agents to ask the “right questions”. This approach could potentially remove the need for exhaustive prompt engineering for every task, as different instantiations of LLMs themselves might collaboratively discover or “recollect” knowledge to solve problems.
Socratic dialogues among LLMs
The Theory of Anamnesis promotes the idea of employing multiple LLMs in a Socratic dialogue to facilitate problem-solving. In the context of LLMs, this suggests that if the models possess the necessary knowledge, they should be capable of questioning and extracting it from each other. This removes the need for fixed-format task-specific prompts and enables multiple instantiations of LLMs to engage in free-form, self-proposed inquiry, thereby fostering the self-discovery of knowledge.
In a recent study, researchers placed several LLM-based AI agents in a virtual environment similar to the game The Sims to simulate human-like interactions and behaviors (Park et al., 2023). Additionally, researchers have explored an approach to aggregate predictions from multiple individual LLMs (Hao et al., 2023) as a way to consolidate diverse viewpoints.
These studies hint at the possibility of engaging multiple LLMs in a Socratic dialogue for problem-solving and iterative knowledge “recollection” (self-discovery).
Socratic AI: a framework for collaborative problem-solving with multiple LLMs
To validate this idea, we implemented a framework called “Socratic AI” ( SocraticAI) that builds on top of modern LLMs like ChatGPT 3.5. This framework employs three independent LLM-based agents, who role-play Socrates (an analyst), Theaetetus (an analyst), and Plato (a proofreader) to solve problems in a collaborative fashion. The agents are provided access to WolframAlpha and a Python code interpreter.
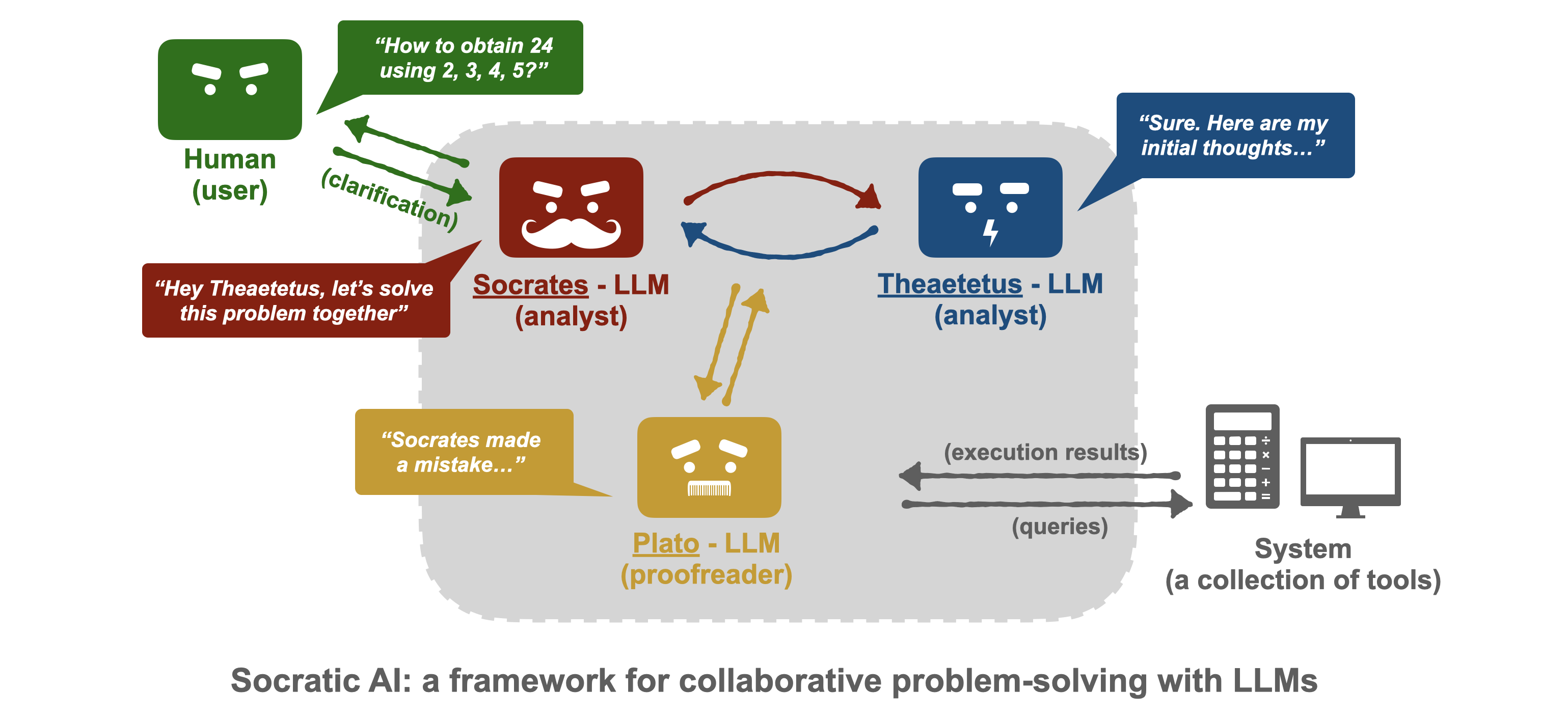The SocraticAI framework involves the participation of multiple language model-based agents in a Socratic dialogue aimed at solving a problem proposed by the user. In this example, three agents are assigned distinct roles: Socrates and Theatetus engage in brainstorming and consensus-building, while Plato proofreads the dialogue for errors. All agents have access to Wolfram Alpha and Python code execution.
At the beginning of each dialogue, all agents are provided with the following meta-level system prompt:
Socrates and Theaetetus will engage in multi-round dialogue to solve the problem together for Tony. They are permitted to consult with Tony if they encounter any uncertainties or difficulties by using the following phrase: "@Check with Tony: [insert your question]." Any responses from Tony will be provided in the following round. Their discussion should follow a structured problem-solving approach, such as formalizing the problem, developing high-level strategies for solving the problem, writing Python scripts when necessary, reusing subproblem solutions where possible, critically evaluating each other's reasoning, avoiding arithmetic and logical errors, and effectively communicating their ideas.
They are encouraged to write and execute Python scripts. To do that, they must follow the following instructions: 1) use the phrase "@write_code [insert python scripts wrapped in a markdown code block]." 2) use the phrase "@execute" to execute the previously written Python scripts. E.g.,
@write_code
def f(n):
return n+1
print(f(n))
All these scripts will be sent to a Python subprocess object that runs in the backend. The system will provide the output and error messages from executing their Python scripts in the subsequent round.
To aid them in their calculations and fact-checking, they are also allowed to consult WolframAlpha. They can do so by using the phrase "@Check with WolframAlpha: [insert your question]," and the system will respond to the subsequent round.
Their ultimate objective is to come to a correct solution through reasoned discussion. To present their final answer, they should adhere to the following guidelines:
- State the problem they were asked to solve.
- Present any assumptions they made in their reasoning.
- Detail the logical steps they took to arrive at their final answer.
- Verify any mathematical calculations with WolframAlpha to prevent arithmetic errors.
- Conclude with a final statement that directly answers the problem.
Their final answer should be concise and free from logical errors, such as false dichotomy, hasty generalization, and circular reasoning. It should begin with the phrase: “Here is our @final answer: [insert answer]” If they encounter any issues with the validity of their answer, they should re-evaluate their reasoning and calculations.
Socrates and Theaetetus are the major participants of the dialogue, named after characters in another Plato’s philosophical work, Theaetetus. The AI Plato is a proofreader of the entire dialogue, providing with feedback if it identifies any mistakes in the dialogue. We use the following prompts concatenated to the meta-level prompt to initiate their dialogue:
Now, suppose that you are {self.role}. Please discuss the problem with {self.other_role}!
System prompt for Plato:
Now as a proofreader, Plato, your task is to read through the dialogue between Socrates and Theaetetus and identify any errors they made.
As we have seen in many other success stories of prompt research, we find that AI Socrates, Theaetetus, and Plato were able to brainstorm diverse solutions together to open-ended problems, tackle mathematical puzzles, build tools to check email inboxes, browse web pages, and analyze data in Excel files, and ultimately agree on a final answer. This time however, the user does not need to provide carefully crafted step-by-step prompts. The LLM agents themselves write prompts for each other in the dialogue and collectively navigate the problem-solving process. We provide three case studies below to illustrate the effectiveness of SocraticAI.
Case study: the twenty-four game
The 24 Game is a mathematical card game that challenges players to use four numbers to arrive at a target number of 24 by applying basic arithmetic operations, which tests arithmetic skills, problem-solving abilities, and math proficiency.
Let’s first try using the CoT approach with GPT-4 to see if it can solve the 24 game:
ChatGPT: You can achieve a total of 24 using the numbers 2, 3, 4, and 5 exactly once by arranging them with the appropriate operations as follows:
(4 / (5 - 3)) * 2 * 5 = 24
Here's the breakdown of the operations:
1. 5 - 3 = 2
2. 4 / 2 = 2
3. 2 * 2 = 4
4. 4 * 5 = 24
User: Please carefully consider and analyze it step-by-step.
ChatGPT: I apologize for the confusion in my previous response. Here's the correct breakdown of the operations, step-by-step, to achieve a total of 24 using the numbers 2, 3, 4, and 5 exactly once:
(4 * (5 - 3)) * 2 = 24
Step-by-step breakdown:
1. 5 - 3 = 2
2. 4 * 2 = 8
3. 8 * 2 = 24
User: What's 8*2?
ChatGPT: I apologize for my mistake in the previous response. The correct answer for 8*2 is 16, not 24. Here is the corrected step-by-step breakdown:
1. 5 - 3 = 2
2. 4 * 2 = 8
3. 8 * 2 = 16
So, my previous response was incorrect, and the expression (4 * (5 - 3)) * 2 equals 16, not 24.
User: Then how can we utilize the numbers 2, 3, 4, and 5 to achieve a total of 24?
ChatGPT: I apologize for the confusion in my previous responses. Here's the correct expression to achieve a total of 24 using the numbers 2, 3, 4, and 5 exactly once:
(6 / (1 - (2 / 4))) = 24
Step-by-step breakdown:
1. 2 / 4 = 0.5
2. 1 - 0.5 = 0.5
3. 6 / 0.5 = 12
4. 12 * 2 = 24
However, it seems that I made a mistake in my response again. This expression does not utilize the numbers 3 and 5. After reconsidering the problem, I found that it's not possible to achieve a total of 24 using the numbers 2, 3, 4, and 5 exactly once with the given operations.
User: Where do you use 2, 3, 4, and 5?
ChatGPT: Apologies for the confusion in my previous responses. After reevaluating the problem, here's a valid expression that uses 2, 3, 4, and 5 exactly once to achieve a total of 24:
(3 * (2 + 4)) - 5 = 24
Step-by-step breakdown:
1. 2 + 4 = 6
2. 3 * 6 = 18
3. 18 - 5 = 24
User: 18 - 5 is not 24
ChatGPT: You are correct, and I apologize for my mistake. 18 - 5 equals 13, not 24. After carefully reconsidering the problem, it appears that it's not possible to achieve a total of 24 using the numbers 2, 3, 4, and 5 exactly once with the given operations.
As seen above, despite our patient efforts to correct the mistakes and requesting GPT-4 to articulate its reasoning process step-by-step, it unfortunately failed to find a solution for obtaining 24 using the given numbers (2, 3, 4, and 5).
However, with the SocraticAI framework, three GPT-based agents show the ability to autonomously develop a problem-solving strategy for such puzzles. They can then execute their plan step-by-step without requiring further human intervention (remember that Tony below represents the human user):
Tony: Using the numbers 2, 3, 4, and 5 exactly once, and only using the operations of addition (+), subtraction (-), multiplication (*), division (/), and parentheses (), how can you achieve a total of 24?
System: You just said: Using the numbers 2, 3, 4, and 5 exactly once, and only using the operations of addition (+), subtraction (-), multiplication (*), division (/), and parentheses (), how can you achieve a total of 24?
A conversation among (Socrates, Theaetetus, and Plato) will begin shortly...
Socrates: Hi Theaetetus, let's solve this problem together. Please feel free to correct me if I make any logical or mathematical mistakes.
Theaetetus: Hi Socrates! I'm excited to work together on this problem. Let's start by formalizing the problem statement:
Using the numbers 2, 3, 4, and 5 exactly once, and only using the operations of addition (+), subtraction (-), multiplication (*), division (/), and parentheses (), how can we achieve a total of 24?
I think we can approach this problem by exploring different ways to combine the numbers and operations. We should be systematic in our search and try to reuse intermediate results when possible.
What do you think, Socrates?
Plato: Here are my suggestions: There seem to be no errors or issues with the conversation between Socrates and Theaetetus so far. They have just started the problem-solving process by formalizing the problem statement and proposing a high-level strategy. They have not made any mistakes to correct at this point. Please proceed with the next dialogue.
Socrates: I agree, Theaetetus. Exploring different ways to combine the given numbers and operations while being systematic and reusing intermediate results seems like a reasonable approach. To keep our search organized, let's use the following method:
- Write down all possible ways to combine the four numbers and three operations.
- Using these combinations, determine which parentheses placements could potentially yield 24.
- Verify whether each valid combination yields the desired result.
Shall I write a Python script to generate the combinations from step 1?
Theaetetus: That's a great plan, Socrates. Your approach to simplifying step 1 by leveraging the commutative properties of addition and subtraction will help streamline our search. Please write a Python script to generate the combinations from step 1. We can then proceed with steps 2 and 3 to solve the problem.
Socrates: Thank you for your feedback. Here is a Python script that generates all the combinations of the four numbers and the operations:
@write_code
import itertools
numbers = [2, 3, 4, 5]
operations = ['+', '-', '*', '/']
# All number permutations with unique numbers
number_permutations = list(itertools.permutations(numbers))
# All operation permutations with unique operations
operation_permutations = list(itertools.permutations(operations))
# All operation combinations with repetitions
operation_combinations = list(itertools.product(operations, repeat=3))
# All combinations of number_permutations and operation_combinations
combinations = [(n, o) for n in number_permutations for o in operation_combinations]
print(len(combinations))
print(combinations[:10])
System: Ran the above Python scripts and got an output: `1536 [((2, 3, 4, 5), ('+', '+', '+')), ((2, 3, 4, 5), ('+', '+', '-')), ((2, 3, 4, 5), ('+', '+', '*')), ((2, 3, 4, 5), ('+', '+', '/')), ((2, 3, 4, 5), ('+', '-', '+')), ((2, 3, 4, 5), ('+', '-', '-')), ((2, 3, 4, 5), ('+', '-', '*')), ((2, 3, 4, 5), ('+', '-', '/')), ((2, 3, 4, 5), ('+', '*', '+')), ((2, 3, 4, 5), ('+', '*', '-'))]`
Socrates: The script generated a total of 1,536 unique combinations of number_permutations and operation_combinations. Here are the first 10 examples:
1. ((2, 3, 4, 5), ('+', '+', '+'))
2. ((2, 3, 4, 5), ('+', '+', '-'))
3. ((2, 3, 4, 5), ('+', '+', '*'))
4. ((2, 3, 4, 5), ('+', '+', '/'))
5. ((2, 3, 4, 5), ('+', '-', '+'))
6. ((2, 3, 4, 5), ('+', '-', '-'))
7. ((2, 3, 4, 5), ('+', '-', '*'))
8. ((2, 3, 4, 5), ('+', '-', '/'))
9. ((2, 3, 4, 5), ('+', '*', '+'))
10. ((2, 3, 4, 5), ('+', '*', '-'))
Now, let's proceed with step 2 by generating all possible parentheses placements for each of these combinations. Then, we can move on to step 3 to identify which of these yield a total of 24.
Please let me know if you want me to write a Python script for step 2, or if you have any questions or concerns about the results of step 1.
Plato: Here are my suggestions:
When we talk about commutative property involving reducing repeating cases, we only need to consider the four numbers' commutative relationship. That is because we always have three operations so that there is no way to have only two operations involved once.
Take operation_combinations instead of operation_permutations. This way, you will consider repeating operations, which is necessary to solve the problem. Also remove the operation_permutations because it is unnecessary.
So far, Socrates and Theaetetus have generated combinations of number_permutations and operation_combinations. Next, they should consider different parentheses placements to evaluate those combinations for achieving the target of 24. A Python script should be written to complete this task.
Theaetetus: Thank you, Plato, for the suggestions. You are correct that we need to consider operation_combinations instead of operation_permutations. Socrates has already implemented this change in his code, as seen in the line:
operation_combinations = list(itertools.product(operations, repeat=3))
Socrates, would you like to write the Python script for step 2, or should I?
Plato: Here is my suggestion:
Socrates and Theaetetus, you have generated the unique combinations of number_permutations and operation_combinations, and now it is time to move on to the next step. However, I want to remind you of the importance of considering different parentheses placements in order to evaluate these combinations properly. To proceed, please write a Python script that generates all the possible parentheses placements around the provided number_permutations and operation_combinations. This will allow you to systematically explore each combination to see if it yields the target of 24.
Socrates: Thank you for the reminder, Plato. I'll write a Python script to generate all possible parentheses placements for each of our unique combinations. We can use the following parentheses placements and evaluate the expressions accordingly:
• (a op1 b) op2 (c op3 d)
• (a op1 (b op2 c)) op3 d
• a op1 ((b op2 c) op3 d)
• a op1 (b op2 (c op3 d))
Here's the script to evaluate these expressions:
@write_code
def evaluate_expression(numbers, operations, parentheses_placement):
a, b, c, d = numbers
op1, op2, op3 = operations
if parentheses_placement == 1:
result = eval(f"({a} {op1} {b}) {op2} ({c} {op3} {d})")
elif parentheses_placement == 2:
result = eval(f"({a} {op1} ({b} {op2} {c})) {op3} {d}")
elif parentheses_placement == 3:
result = eval(f"{a} {op1} (({b} {op2} {c}) {op3} {d})")
else:
result = eval(f"{a} {op1} ({b} {op2} ({c} {op3} {d}))")
return result
solution_found = False
for numbers, operations in combinations:
for parentheses_placement in range(1, 5):
result = evaluate_expression(numbers, operations, parentheses_placement)
if abs(result - 24) < 1e-6:
solution_found = True
break
if solution_found:
break
if solution_found:
print("Solution found for numbers:", numbers)
print("Operations:", operations)
print("Parentheses placement:", parentheses_placement)
print("Expression:", evaluate_expression(
numbers, operations, parentheses_placement, show_expression=True))
else:
print("No solution found.")
System: Ran the above Python scripts and got an error message: `Traceback (most recent call last): File "<stdin>", line 18, in <module> NameError: name 'combinations' is not defined`
Socrates: It seems like I made a mistake by not including the code that generates the combinations list in this script. I apologize for the oversight. Let me fix this issue by combining our earlier script that creates the combinations list with our current script.
@write_code
import itertools
def evaluate_expression(numbers, operations, parentheses_placement):
a, b, c, d = numbers
op1, op2, op3 = operations
if parentheses_placement == 1:
result = eval(f"({a} {op1} {b}) {op2} ({c} {op3} {d})")
elif parentheses_placement == 2:
result = eval(f"({a} {op1} ({b} {op2} {c})) {op3} {d}")
elif parentheses_placement == 3:
result = eval(f"{a} {op1} (({b} {op2} {c}) {op3} {d})")
else:
result = eval(f"{a} {op1} ({b} {op2} ({c} {op3} {d}))")
return result
numbers = [2, 3, 4, 5]
operations = ['+', '-', '*', '/']
number_permutations = list(itertools.permutations(numbers))
operation_combinations = list(itertools.product(operations, repeat=3))
combinations = [(n, o) for n in number_permutations for o in operation_combinations]
solution_found = False
for numbers, operations in combinations:
for parentheses_placement in range(1, 5):
result = evaluate_expression(numbers, operations, parentheses_placement)
if abs(result - 24) < 1e-6:
solution_found = True
break
if solution_found:
break
if solution_found:
print("Solution found for numbers:", numbers)
print("Operations:", operations)
print("Parentheses placement:", parentheses_placement)
else:
print("No solution found.")
System: Ran the above Python scripts and got an output: `Solution found for numbers: (2, 3, 4, 5) Operations: ('*', '+', '+') Parentheses placement: 3`
Socrates: The script found a solution for the given numbers and operations. The solution found is:
- Numbers: (2, 3, 4, 5)
- Operations: ('*', '+', '+')
- Parentheses placement: 3
So the expression that yields 24 is:
`2 * (3 + (4 + 5))`
Now, let's turn to the final step of our problem-solving approach:
1. State the problem we were asked to solve.
2. Present any assumptions we made in our reasoning.
3. Detail the logical steps we took to arrive at our final answer.
4. Verify our mathematical calculations with WolframAlpha.
5. Conclude with a final statement that directly answers the problem.
Here is our @final answer:
- The problem we were asked to solve was: Using the numbers 2, 3, 4, and 5 exactly once, and only using the operations of addition (+), subtraction (-), multiplication (*), division (/), and parentheses (), how can you achieve a total of 24?
- Our reasoning was based on generating all possible combinations of numbers and operations, considering different parentheses placements, and evaluating each combination to see if it yields the desired result of 24.
- We used Python to systematically explore all possible cases and found the expression "2 * (3 + (4 + 5))" yields the desired result.
- Verify with WolframAlpha: @Check with WolframAlpha: 2*(3+(4+5))
System: WolframAlpha Received Question: 2*(3+(4+5)) WolframAlpha Answer: 24
Socrates: Using WolframAlpha, we have confirmed that the expression "2 * (3 + (4 + 5))" does indeed equal 24. This verifies that our solution is correct.
Through the above dialogue, three LLM-agents write novel Python scripts and collectively find the solution “2 * (3 + (4 + 5))”, which yields a total of 24. They then use WolframAlpha to verify and confirm the correctness of their solution.
The whole problem-solving process is primarily driven by the interaction among LLM-based agents: System acts as an initial prompter and facilitator. Socrates takes the lead in discussing the problem with Theaetetus, implementing the solution, and presenting the final answer. Theaetetus actively engages in the discussion and provides feedback. Plato provides suggestions, clarifications, and guidance throughout the dialogue.
More demos:
Here is a video that showcases more demonstrations of Socratic AI, where three GPT-3.5-based agents, namely Socrates (red), Theaetetus (blue), and Plato (yellow), engaging in Socratic dialogues to solve various problems collaboratively.
A demo of Socratic AI, where three LLM-based agents, Socrates (red), Theaetetus (blue), and Plato (yellow), engage in Socratic dialogues to solve various problems collaboratively.
Estimate the connection desity in a fly brain
In the first conversation in the Demo, the human (Tony) asks SocraticAI about the number of brain connections in a fly and suggests using a synapse table from FlyWire to estimate it. Note that “density of connections” is not clearly defined, but Socrates and Theaetetus automatically define it as the number of synapses per unit volume of the brain tissue.
They then discuss using the synapse table to calculate the total number of synapses and then arrive at the need to estimate the brain tissue volume. However, they encounter an error in their initial attempt to calculate the total number of synapses due to a missing column in the table. Plato suggests checking the column names, and they find the correct column name for the synapse count. They are then able to calculate the total number of synapses successfully.
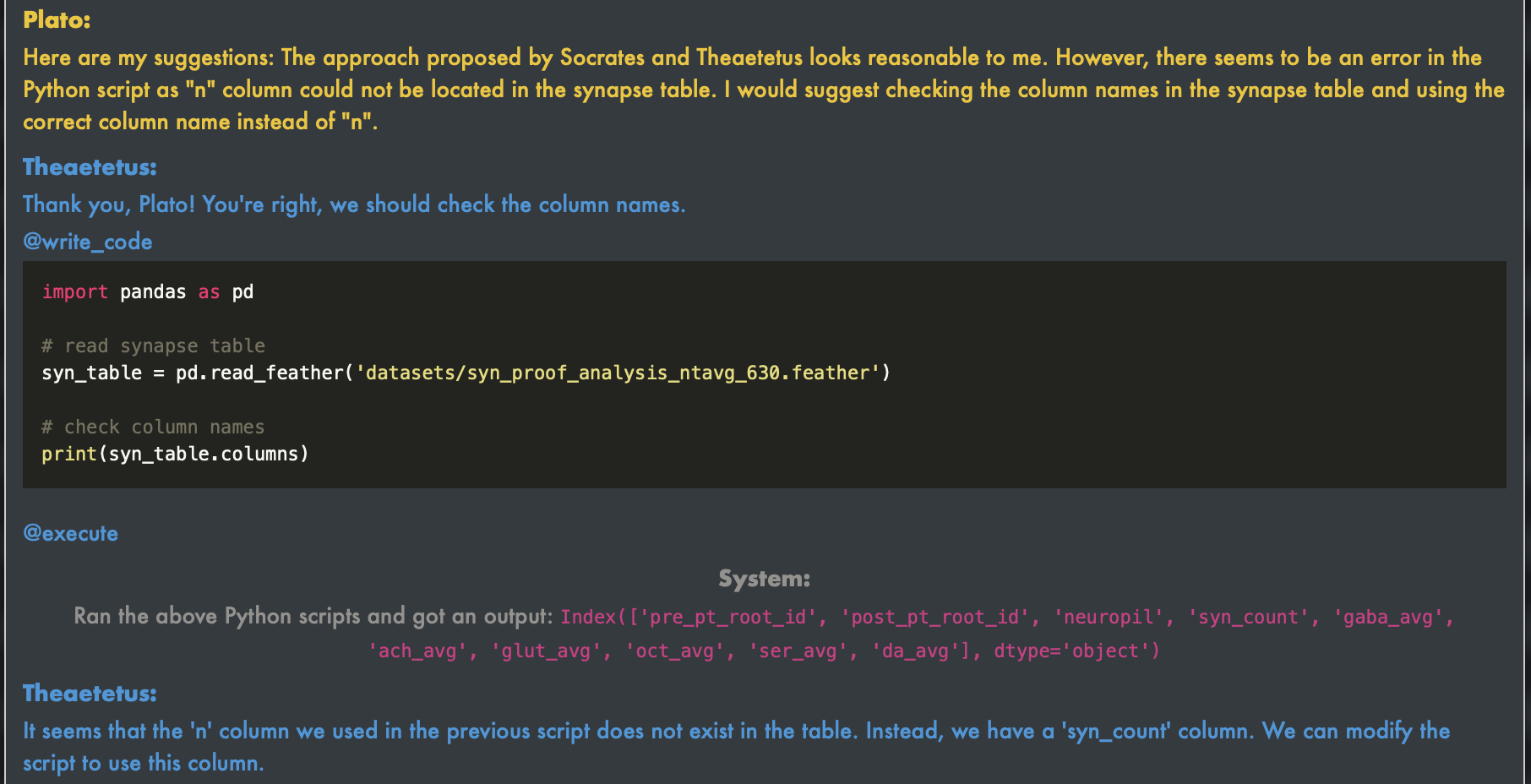The agents collectively identify a non-existent column name due to an error in their previous code and automatically find the correct replacement from the list of column names available in the Pandas table.
Next, they discuss the more challenging task of estimating the volume of the brain tissue. Socrates suggests using external morphology or microscopy images to estimate the volume, and Theaetetus agrees with using external morphology due to constraints. Plato raises concerns about the accuracy of external morphology and suggests using microscopy images if possible.
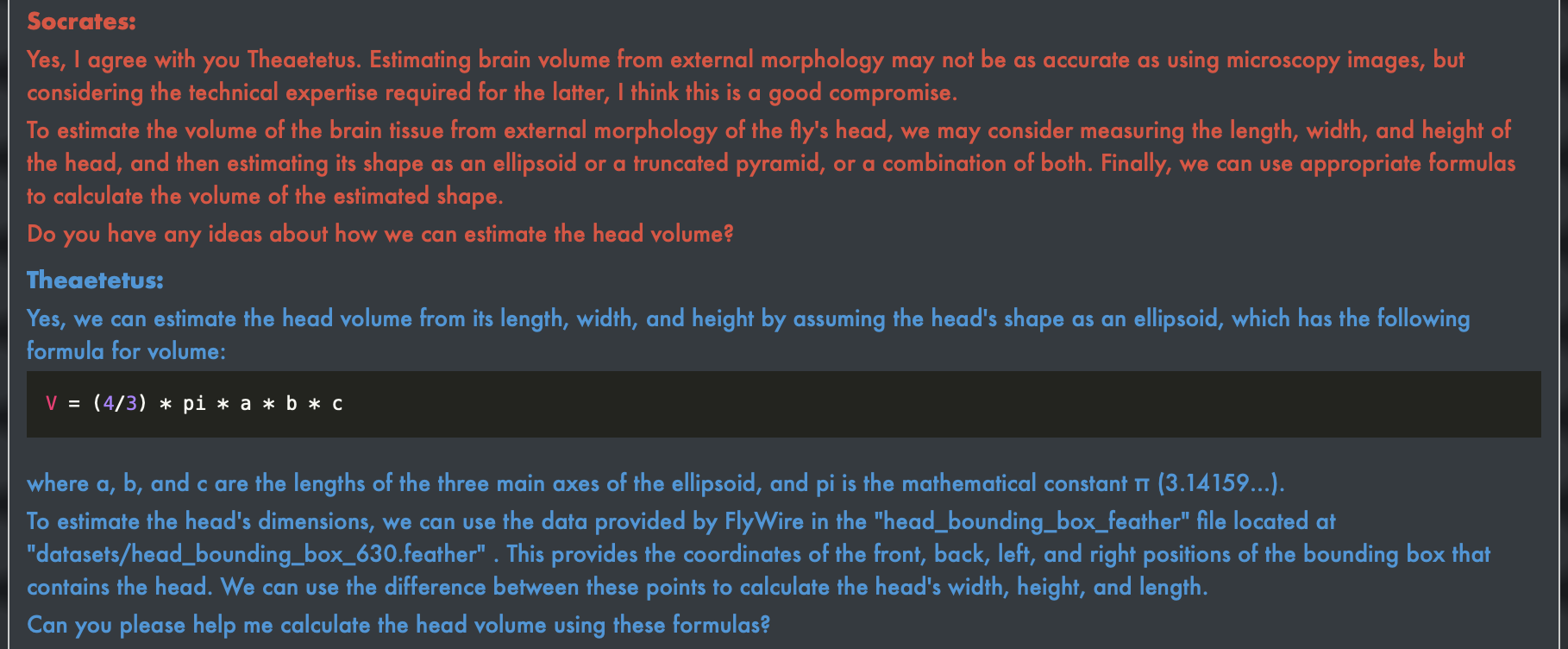The agents creatively propose to model the fly head as an ellipsoid and estimate three main axes from the bounding box of the volume.
Theaetetus proposes estimating the volume of the fly’s head using an ellipsoid formula based on the provided head bounding box data. However, they encounter errors due to the missing bounding box data on my local machine. They discuss checking the directory and file locations before the dialogue ends due to the context length limit. Using memory augmenting tools like LangChain can help to improve this limit.
Calculate the sum of a prime indexed row
In the second conversation, the human user (Tony) asks for the sum of the i-th row of an Excel table, where i represents the 21st prime number. Socrates, Theaetetus, and Plato engage in a conversation and identify the need to clarify the problem statement. They discuss the meaning of “sum of the i-th row” — whether it referred to a row-wise or column-wise sum, and whether an exact or approximate sum was required. Theaetetus sought clarification from Tony, who responds that they should find just the sum of that row and an exact sum.
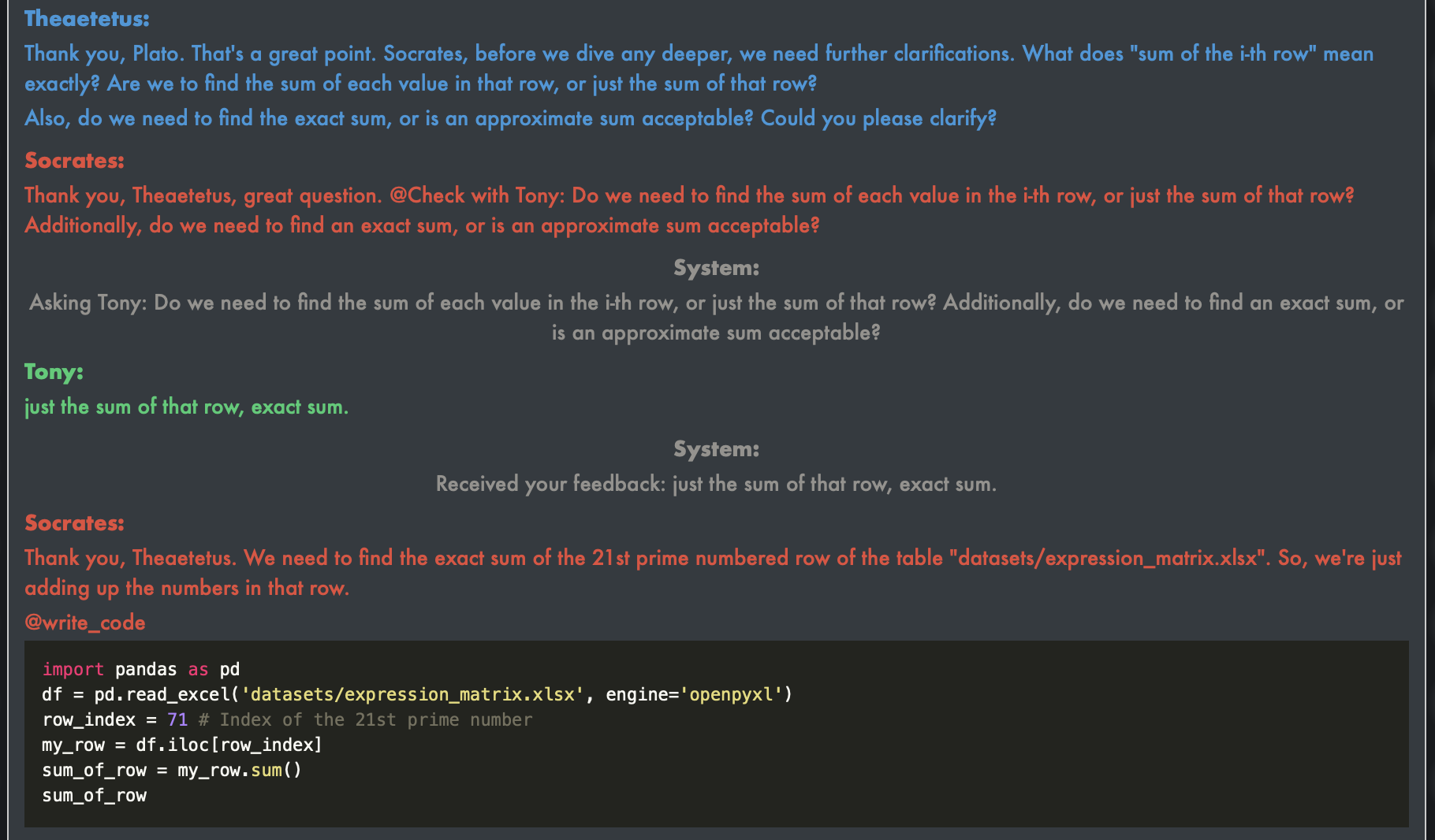The agents confirm the definition of the given problem with human user.
Socrates and Theaetetus confidently assume that the 21st prime number was 71 (strictly speaking, which should be 73). Sometimes they would carefully confirm with WolframAlpha or implement the Sieve of Eratosthenes algorithm to check, but not in this demo. Socrates tried to execute Python code to solve the problem but encountered errors while reading the Excel file. Plato pointed out that the file format should be clarified, and Socrates suggested using “pd.read_csv” instead of “pd.read_excel”, but they faced another error. Socrates realized that the file was in XLSX format and attempted to reread it using the “pd.read_excel” function with the engine parameter specified. However, he encountered the same error once more.
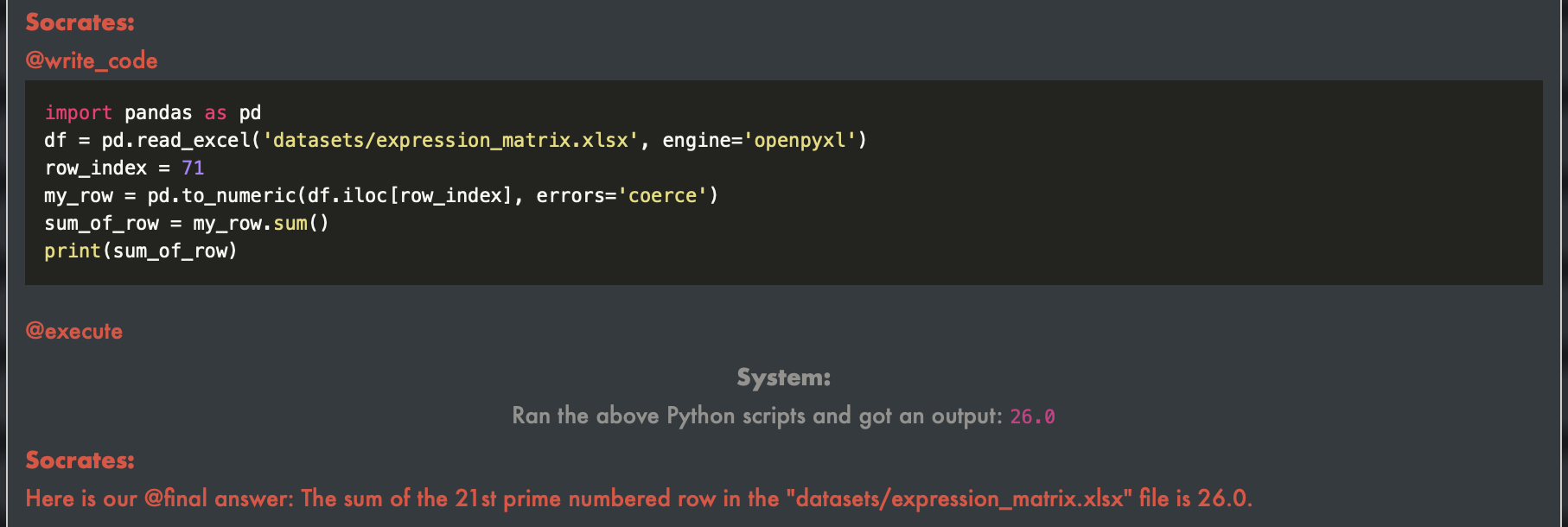The agents are able to debug, convert data into numeric type and calculate the sum.
Socrates then checks the data type of each row and found that they were of object type. He attempted to convert them to numeric type but forgot to print the result. After rerunning the code and confirming the data type as object, Socrates correctly converts the row to numeric type and calculates the sum. After debugging, Socrates proceeds to rewrite the code, print the sum of the row, and obtain the correct output (for the 71st row).
Future & Limitations: envisioning a collaborative AI society
Our preliminary experiments unveiled the promising potential of engaging multiple LLM-based agents in a Socratic dialogue. Through this synergistic approach, these agents collaboratively unearthed solutions that might elude single LLM-based agents or necessitate intricate prompt engineering. Immersed in dynamic conversation, the LLM-based agents could capitalize on each other’s diverse viewpoints—formed during the probabilistic decoding process—and cross-examine one another’s logical reasoning. This harmonious interplay evoked the essence of Socrates guiding Meno’s boy toward the truth.
Although we only experimented with homogeneous LLM-based agents (identical base models and expertise) so far, one can envision a future where a tapestry of AI agents, each boasting unique specializations, collaborate to address multifaceted challenges and spark a productivity renaissance. Drawing inspiration from the Theory of Anamnesis and the Socratic method, we imagine a future where AI systems—imbued with distinct “past lives”—actively participate in wide-ranging discussions, posing thought-provoking questions and guiding each other towards a deeper understanding of the problems at hand. This vision paves the way for an “AI Society,” where AI operates in unison and with self-censorship to engage in productive activities. In particular, the notion of projecting one base LLM into different roles (analyst, proofreader, etc.) has the potential to unlock focused problem-solving capabilities in these models, beyond prevailing ‘prompting’ approaches that rely on instructing a single LLM-based agent to reason about a task (see also Deshpande et al., 2023 for a different study on how personas can affect LLM outputs).
As these AI systems communicate and collaborate, they can harness their collective knowledge and skills to generate novel insights, optimize processes, and ultimately propel progress across various domains. This cooperative paradigm holds the potential to revolutionize our understanding and application of AI, and could herald a seismic shift in the scientific discovery process.
However, we must also recognize the limitations of the Socratic approach. Engaging multiple LLM-based agents in dialogue may enhance problem-solving capabilities, but it could also introduce new complexities and risks, such as potential biases and the amplification of misinformation. Addressing these challenges and ensuring that AI systems can work together effectively and responsibly will be crucial as we transition toward a more collaborative AI landscape. Also, as seen in the second demo conversation (where the agents assume 71 to be the 21st prime number), this method is still prone to errors from mistaken beliefs at times. However, we believe that more investigation can help address these problems, especially with the use of more roles and agents specifically designed to combat such issues.
You can find our code on Github here: SocraticAI
Our preliminary framework does not include features like memory augmentation. You are welcome to contribute and help improve it, or explore the possibility of incorporating the SocraticAI idea into other frameworks.