MeZO: Fine-Tuning Language Models with Just Forward Passes

November 14, 2023 | Written by Sadhika Malladi and Tianyu Gao | [Paper][Code]

Fine-tuning pre-trained language models (LMs) was introduced as an effective method to rapidly adapt highly capable models to solve many language tasks, adapt to specialized domains, or incorporate human instructions and preferences. However, as LMs are scaled up, computing gradients for backpropagation requires a prohibitive amounts of memory – in our test, up to 12× the memory required for inference. This is because we need to cache activations during the forward pass, gradients during the backward pass, and, sometimes even store gradient history (e.g., for Adam).

This work introduces a memory-efficient zeroth-order optimizer, MeZO, that fine-tunes LMs using only forward passes, thereby requiring the same amount of memory as what’s needed for inference. Despite using substantially less memory, MeZO achieves performance within 1% absolute of standard fine-tuning on most tasks. And, contrary to classical theoretical intuitions, MeZO can efficiently optimize models with up to 66B parameters while using fewer GPU-hours than traditional fine-tuning. Moreover, MeZO can optimize non-differentiable objectives like accuracy, F1, or potentially, scores from a reward model.

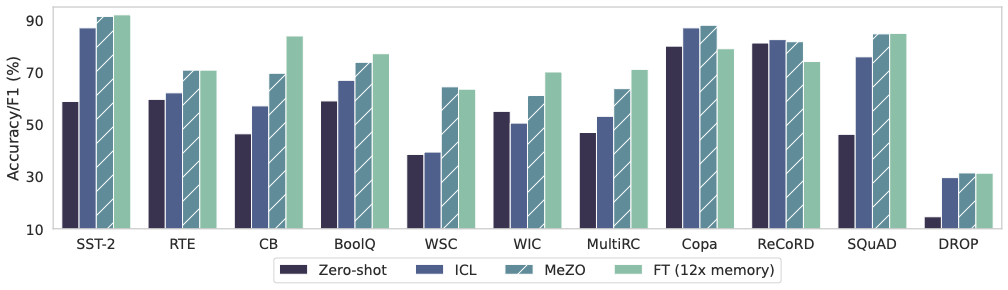
Comparison of MeZO to zero-shot, in-context learning (ICL), and standard fine-tuning of OPT-13B. MeZO performs within 1% absolute of fine-tuning on 7 out of11 tasks despite using substantially less memory.

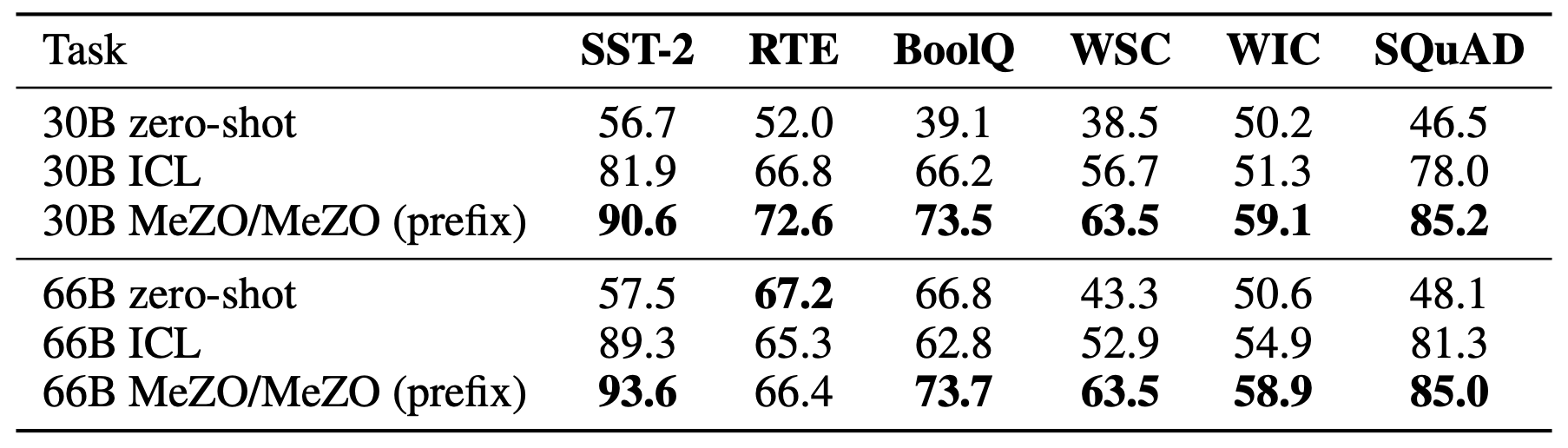
Contrary to classical analyses that suggest zeroth-order methods are proportionally slow for more parameters, MeZO successfully optimizes OPT models of up to 66B and outperforms zero-shot and in-context learning.

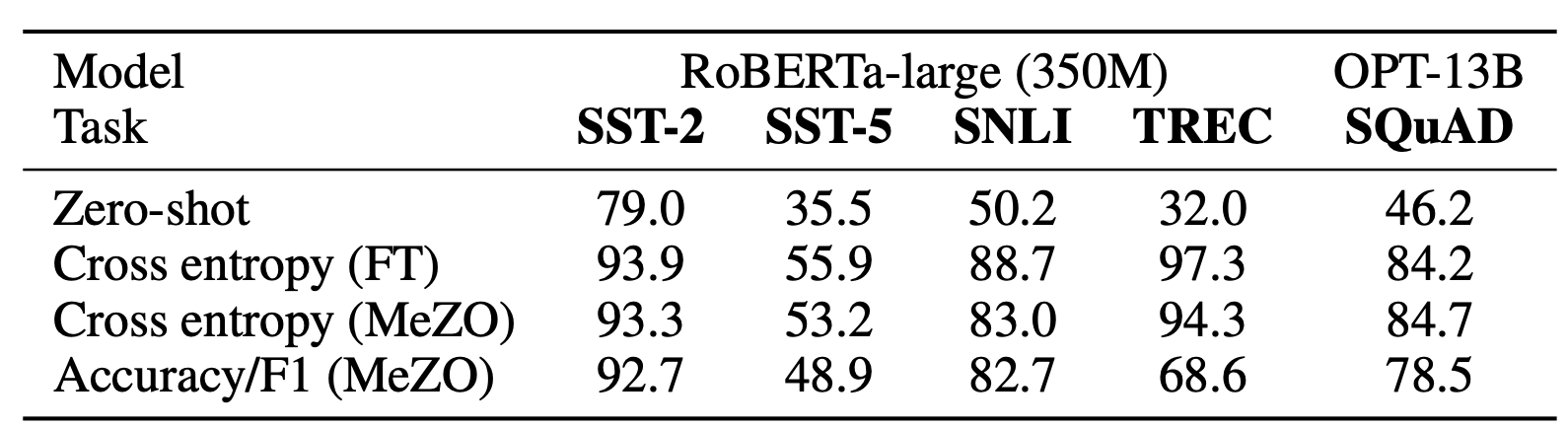
Unlike backpropagation, MeZO can optimize any objective function, even the non-differentiable ones. For classification tasks (512 examples per class), we use accuracy as the objective; for SQuAD (1,000 examples), we use F1 as the objective.

Motivation

Fine-tuning with Adam can require up to 12x the memory needed for inference. As a result, one usually needs a lot more GPUs to fine-tune a model than what’s needed to serve it. Even parameter-efficient fine-tuning methods, like prefix tuning and LoRA, require much more memory than inference does. This makes it difficult to fine-tune large, performant pre-trained LLMs.

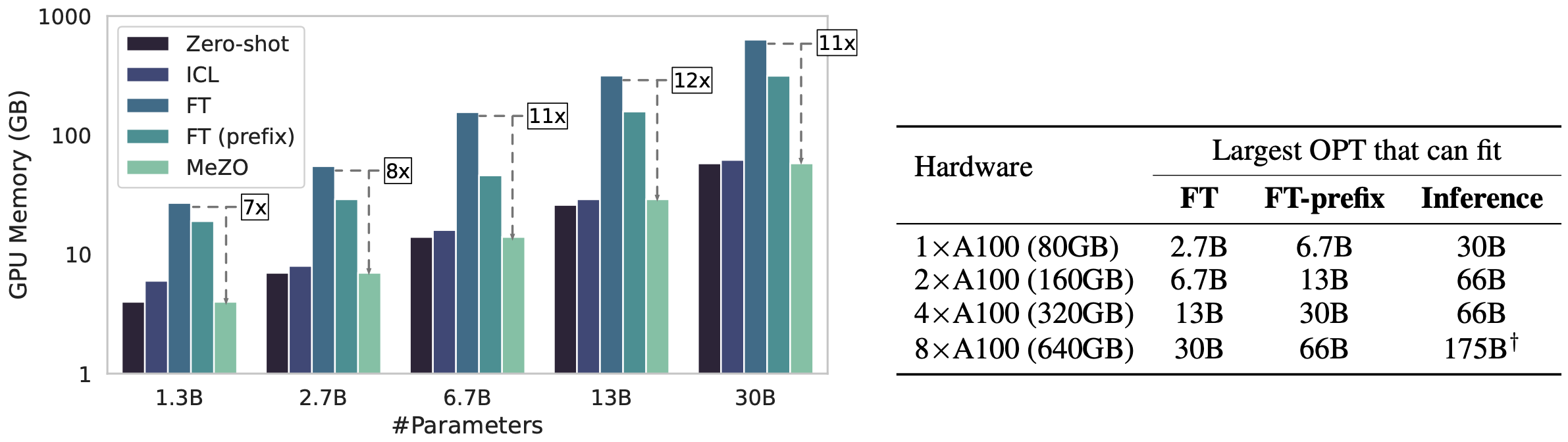
The figure and table above show GPU profiling results of OPT models with different sizes and different methods. Profiling is done on the MultiRC dataset (400 tokens per example on average).

Other disadvantages to fine-tuning via backpropagation include:

1. Differentiable objective: Running backpropagation requires a differentiable objective. This has driven the paradigm of minimizing surrogate differentiable losses instead of directly maximizing accuracy. Analogously, when incorporating human feedback and preferences, one often has to resort to reinforcement learning (Ouyang et al., 2022).
2. Communication overhead: Large models require training on more than 1 GPU. In this case, model weights, activations, and gradients must be frequently synced across GPUs, which introduces a large communication overhead.
3. Gradient history: Optimizers like Adam and SGD with momentum require access to past gradients in order to update the model. Storing these gradients directly further increases the memory cost.

MeZO Algorithm

MeZO computes gradients using a classical zeroth-order method called SPSA (Spall, 1992). For a loss function $\mathcal{L}(\theta;B)$ evaluated on batch $B$ using model parameters $\theta$, we estimate the gradient as:

[[ \hat\nabla\mathcal L(\theta; B) = \frac{\mathcal{L}(\theta+\epsilon z; B) - \mathcal{L}(\theta-\epsilon z; B)}{2\epsilon} z ]]

where $z$ is an i.i.d. Gaussian perturbation applied element-wise to the parameters and $\epsilon$ controls the strength of the perturbation. This formula can be interpreted as evaluating the gradient in just one direction determined by $z$.

MeZO requires two forward passes to evaluate the loss function using the perturbed parameters. A straightforward implementation of the algorithm would require storing $z$, which is just as large as the model $\theta$, on the GPU. MeZO adapts this algorithm to operate in-place by saving the random seed and resampling $z$ whenever it’s needed. So, the gradient can be computed and applied to each parameter without consuming any additional memory.

It is easy to see how MeZO addresses some of the shortcomings of backpropagation:

1. Differentiable objective: The gradient estimate only requires evaluating $\mathcal{L}$, so MeZO can optimize non-differentiable objectives. Preliminary experiments in our paper show that that MeZO can directly maximize accuracy on various tasks for models with up to 66B parameters.
2. Communication overhead: The communication overhead is substantially reduced, because MeZO requires fewer GPUs than standard fine-tuning. As a result, MeZO is more than 7x faster per step and uses half as many GPU-hours as standard fine-tuning on a 30B OPT model. Our paper (Appendix F.6) contains more details about the wall-clock measurement.
3. Gradient history: MeZO can reconstruct gradients from just two scalars: the normalized difference in the loss values and the random seed used to sample $z$. Accessing the gradient history is thus much more memory-efficient, and MeZO even admits accessing gradients from an arbitrary past step. This also allows us to substantially reduce the checkpoint storage cost compared to parameter-efficient methods: saving a fine-tuned 66B parameter model with MeZO requires less than 0.1 MB whereas LoRA requires 38 MB of storage.

When to use MeZO?

You can use MeZO whenever you need to fine-tune a language model with a natural language prompt (the prompt can be as simple as “…. Answer:”). MeZO is especially useful when you are fine-tuning extremely large models and are constrained by GPU memory, as we showed that MeZO can reduce up to 12x memory usage compared to Adam. MeZO may also excel at providing an efficient but fuzzy gradient estimate (e.g., for data selection). Moreover, MeZO can optimize non-differentiable objectives (e.g., human preferences and feedback) as a replacement for more complex algorithms like reinforcement learning.

You probably don’t want to use MeZO if you are working with very small models (e.g., BERT-size), since MeZO converges much slower compared to backpropagation on small models and can still lag behind backpropagation on certain tasks. We also note that MeZO prescribes a distinct optimization trajectory from standard fine-tuning, so it may not be useful for building a mechanistic interpretation of fine-tuning. Also, MeZO is not likely to perform well when you need to introduce new parameters (e.g., a new prediction head for classification) or when you need to pre-train a model from scratch. As we will explain in the next section, the success of MeZO relies on using a pre-trained base model.

Why does it work?

Classical analyses (such as Jamieson et al., 2012; Duchi et al., 2015) have shown that zeroth order methods should require $d$ times as many steps, where $d$ is the number of parameters in the model. For 66B parameter models, this is catastrophic! So, why does MeZO manage to fine-tune models in a reasonable time frame?

In our paper, we suggest that because the model is pre-trained, when we use a simple prompt (e.g., “… Answer: “) with the downstream task, the loss has an intrinsic low-dimensional structure. Intuitively, a straightforward prompt turns the downstream task into a syntactically correct complete-the-sentence task, so it looks a lot like a pre-training example. This avoids the worst case scenario, where one needs gradient information in all $d$ directions in order to optimize the objective. Instead, the slowdown scales with the intrinsic structure of the task. That’s why a prompt is essential in order for MeZO to work!

Acknowledgement: Thanks to our amazing collaborators: Eshaan Nichani, Alex Damian, Jason D. Lee, Danqi Chen, and Sanjeev Arora. Thanks to Eshaan Nichani and Alex Damian for the feedback on the blog post.