
Abstract
In this work, we show that deep neural networks are capable of generating accurate predictions over mixtures of inputs. We introduce data multiplexing (DataMUX), a novel technique that enables networks to process multiple inputs simultaneously using a single compact representation, resulting in increased throughput with minimal extra space requirements. Our approach uses two key components – a multiplexing layer that performs a fixed linear transformation to each input before combining them to create a single `mixed’ representation which is processed by the base network, and a demultiplexing layer that converts the network’s output back into independent representations before producing predictions for each input. We demonstrate the viability of DataMUX for multiple architectures (Transformers, and to a lesser extent MLPs and CNNs) across six different tasks spanning sentence classification, named entity recognition and image classification. For instance, DataMUX for Transformers can multiplex up to 20x/40x, achieving 11x/18x throughput with minimal absolute performance drops of <2% and <4%, respectively over a standard Transformer on MNLI, a natural language inference task.We also provide a theoretical construction for multiplexing in self-attention networks and analyze the effect of various design elements in DataMUX.
Multiplexing for the Transformer
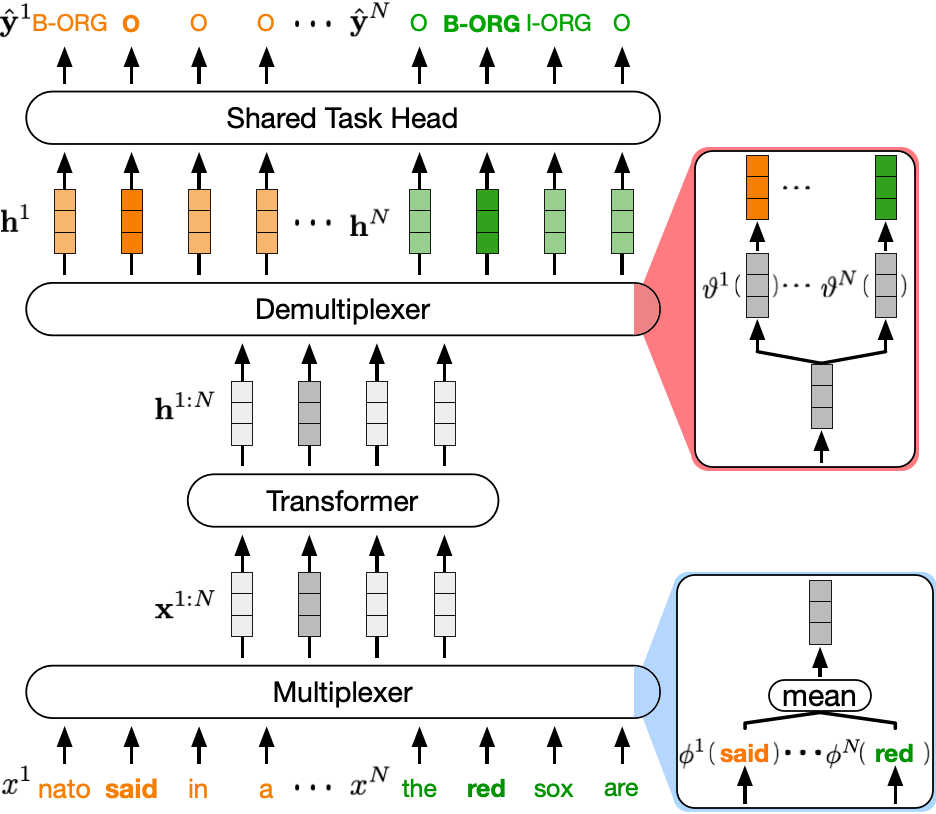
Illustration of DataMUX applied to a Transformer model. Given a tuple of \(N\) sentences (\(x^1, x^2, \dots, x^N\)), each of length \(L\), we first apply a multiplexing operation which performs a transformation \(\phi^i\) on the embeddings of each sequence \(x^i\), such that the same transformation is applied to every token in a sequence \(x^i\). The multiplexing operation then aggregates the sequences by averaging over each position, generating a single combined sequence \(\mathbf{x}^{1:N}\in\mathbb{R}^{L\times d}\), for embedding size \(d\), which will be passed on to the central Transformer model. After processing, we perform a demultiplexing operation to the Transformer model’s output \(\mathbf{h}^{1:N}\in\mathbb{R}^{L\times d}\), to generate hidden representations \(\mathbf{h}^1, \mathbf{h}^2, \dots, \mathbf{h}^N\), corresponding to inputs \(x^1, x^2, x^N\) respectively. We finally use these hidden representations to generate predictions for a particular task (e.g. named entity recognition (NER)) using a shared task prediction head.
Task Performance Results
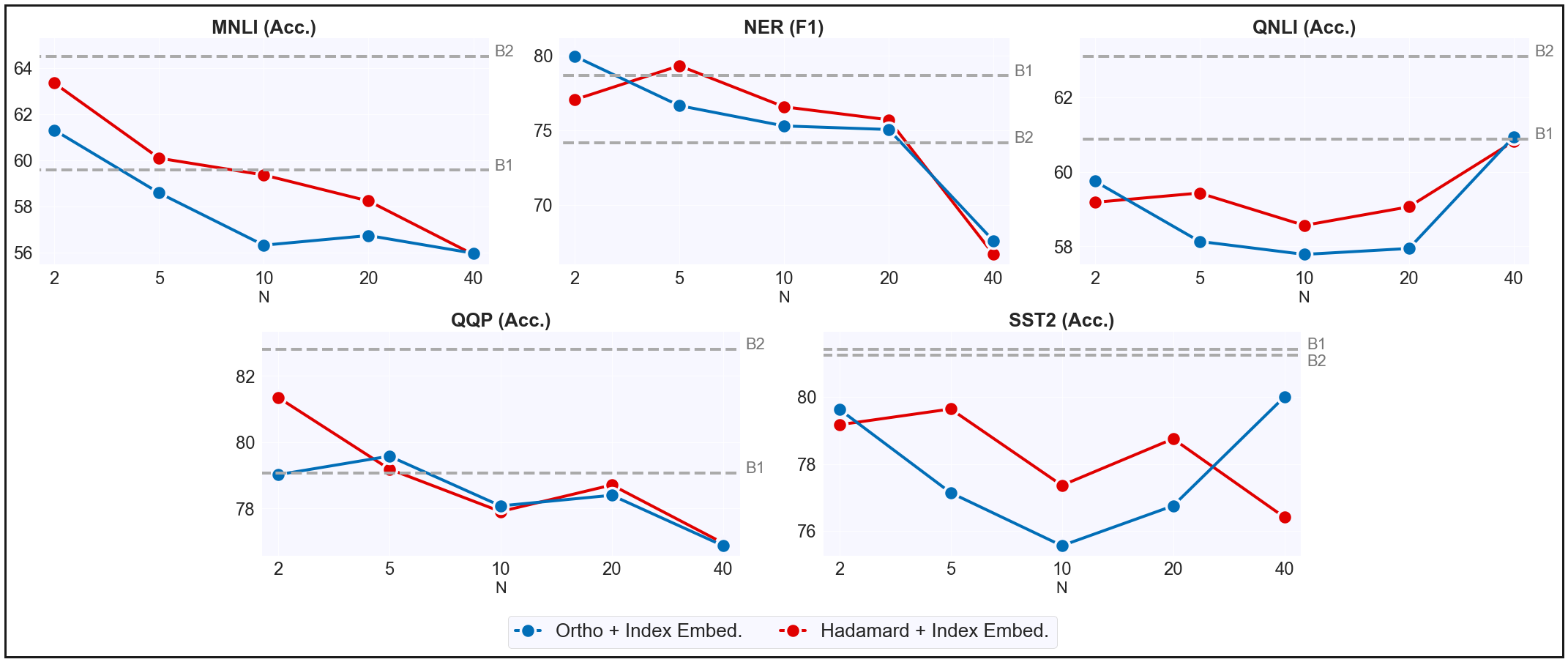
Results for data multiplexing using \(\phi^i\) as an orthogonal matrix or hadamard product. We compare 12-layer DataMUX models to a vanilla 12-layer Transformer (B1) and a Transformer pre-trained using our proposed retrieval task (B2). We demonstrate multiplexing up to \(40\) instances without substantial degradation in task performance.
Throughput Performance Results
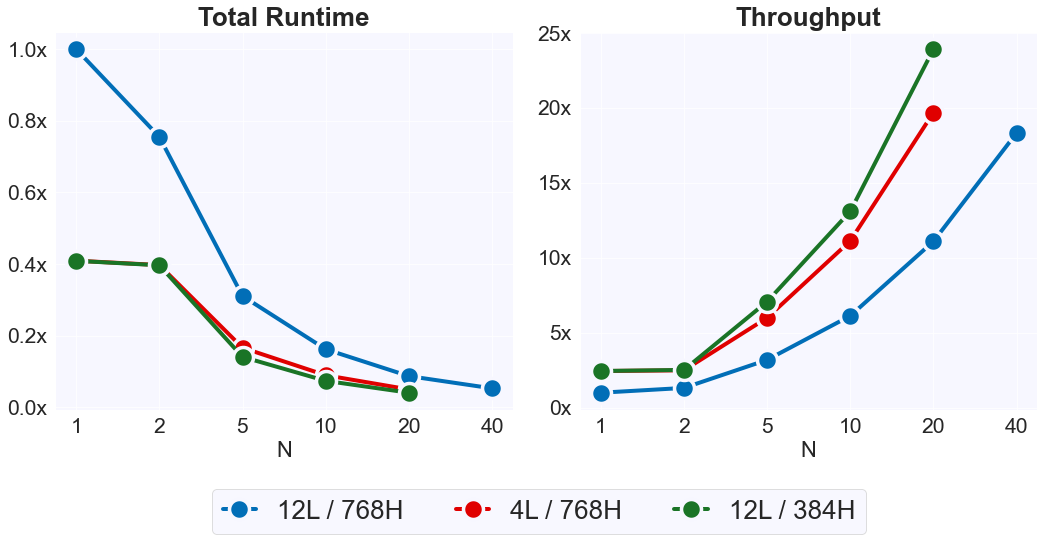
We evaluate the efficiency of DataMUX for models of different sizes on \(20,000\) MNLI instances (\(N=1\) being a vanilla Transformer). The y-axis shows performance normalized by the 12-layer vanilla Transformer model. We demonstrate an \(18\)x throughput increase for \(N=40\) on the 12-layer model and a nearly \(25\)x throughput increase for smaller models with \(N=20\).
Authors
Citation
@inproceedings{
murahari2022datamux,
title={Data{MUX}: Data Multiplexing for Neural Networks},
author={Vishvak Murahari and Carlos E Jimenez and Runzhe Yang and Karthik R Narasimhan},
booktitle={Thirty-Sixth Conference on Neural Information Processing Systems},
year={2022},
url={https://openreview.net/forum?id=UdgtTVTdswg}
}



